| Version 28 (modified by , 6 years ago) (diff) |
|---|
ReferenceNetsReachabilityGraph
Examples for the Reference Net Reachability Graph Plugin
Nets without subnets
The following example shows a simple reference net without any subnets. The reachability graph is generated as expected, with the red node representing the initial marking and any other node representing a reachable marking of the net. The edges are labeled with the respective transition that fired. The inscription can be extended to show the full binding of the firing.
Example
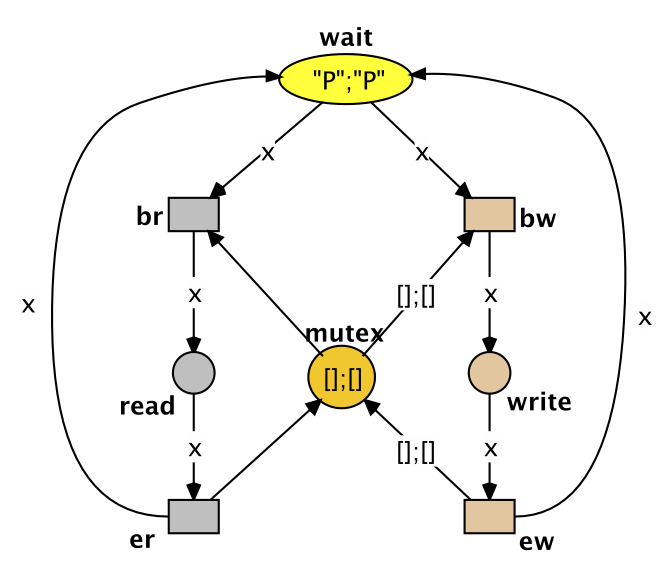
A reference net modeling the reader writer problem with two people and the generated reachability graph. Black tokens are noted as [] .
Depth limited search
If desired, the Reference Net Reachability Graph Plugin can generate the reachability graph only up to a specified depth. The following example shows the same net of the prior example, generated with a depth limit of 1. Here, all markings that can be reached by firing one transition are fully explored. All further bindings that the simulation finds are listed, but not explored. These special unexplored markings are represented by a triangular node. Note that it is possible that an unexplored marking could be identical to one of the already explored markings in the graph. As the markings are not explored however, they are not summarized to one marking.
Example
The same net as before, this time with a depth limit. Possible, but not explored bindings are represented with a triangular node. Bindings of unexecuted bindings are still listed, as can be seen on the lower left edge inscription.
Introducing an unbounded place
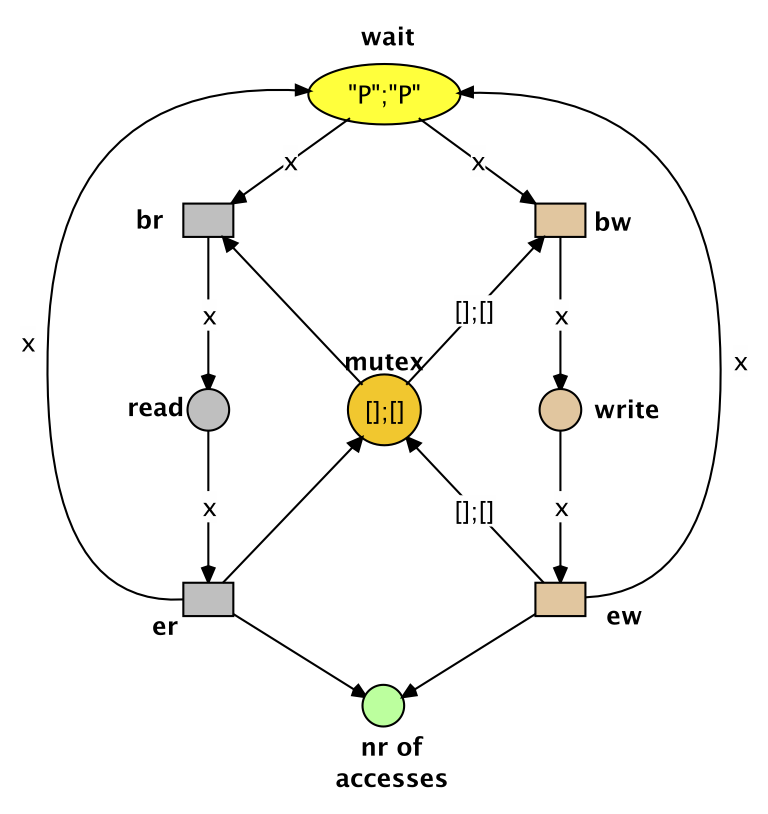
For every distinct state of the root net there is a node in the reachability graph. While common algorithms that create reachability graphs terminate in this case, the ReferenceNetsReachabilityGraph Plugin does not contain a comparison of markings yet. Consequently, if any net contains an unbounded place, an infinite amount of nodes are created in the reachability graph. To illustrate, the previous example has been modified to include a place, which counts how many times the resource in the reader/writer problem has been accessed.
Example
As a result of the newly introduced place, a chain of nodes emerge in the reachability graph, wherein each cycle in the root net results in an additional token in the reachability graph. So although only one place in the net accumulates tokens and the possible transition sequences are irrelevant to the number of tokens in that place, the resulting reachability graph gets infinitely more nodes. It is still possible to visualize a portion of it by setting a depth limit for exploration. However, a better approach to visualize these kinds of state spaces would be the coverability graph, which may come in a later update.
Nets with subnets
The previous example displayed the reachability graph only for a single net without reference to other nets. For the inspection of more complicated and nested nets, we turn off the node inscriptions of the reachability graph and instead explore it interactively.
A graph node represents the root net instance in a certain marking. It can be double-clicked, which will open a copy of the root net instance in this particular marking. This root net instance may itself contain other net instances as tokens (each in a particular marking). In fact, the (marked) net instances in a single graph node can freely contain each other as long as they are reachable from the root net instance. They can be interactively explored in the UI starting from the root net instance by double-clicking net instance tokens.
For any firing that happens within a net instance other than the root net instance, the edge is labeled with the identifier of the net instance proceeding the transition identifier.
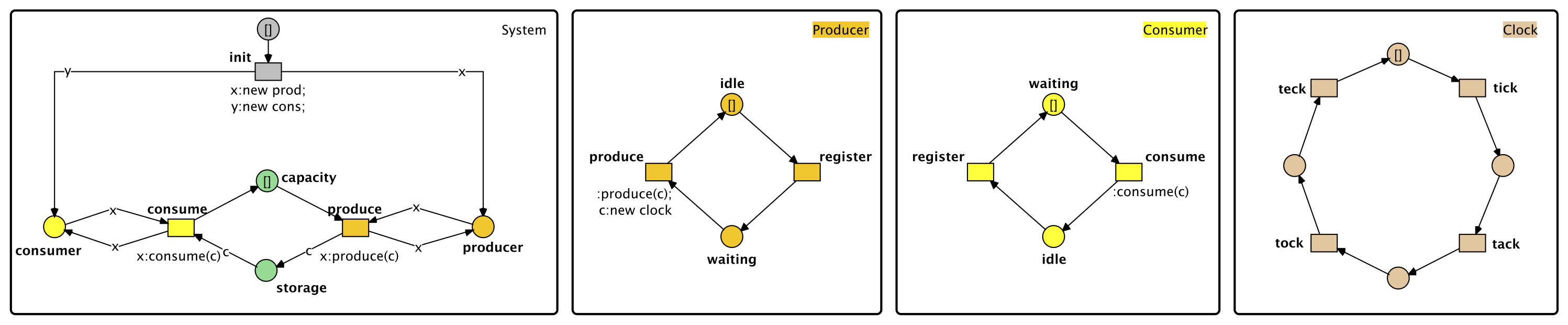
The Producer Consumer Problem
The first example is the classic producer consumer problem (with a storage capacity), where producer and consumer are distributed into an own net each. Their net instances are created in the system net, which also holds the storage place for the producer and consumer. The synchronisation happens via synchronous channels.
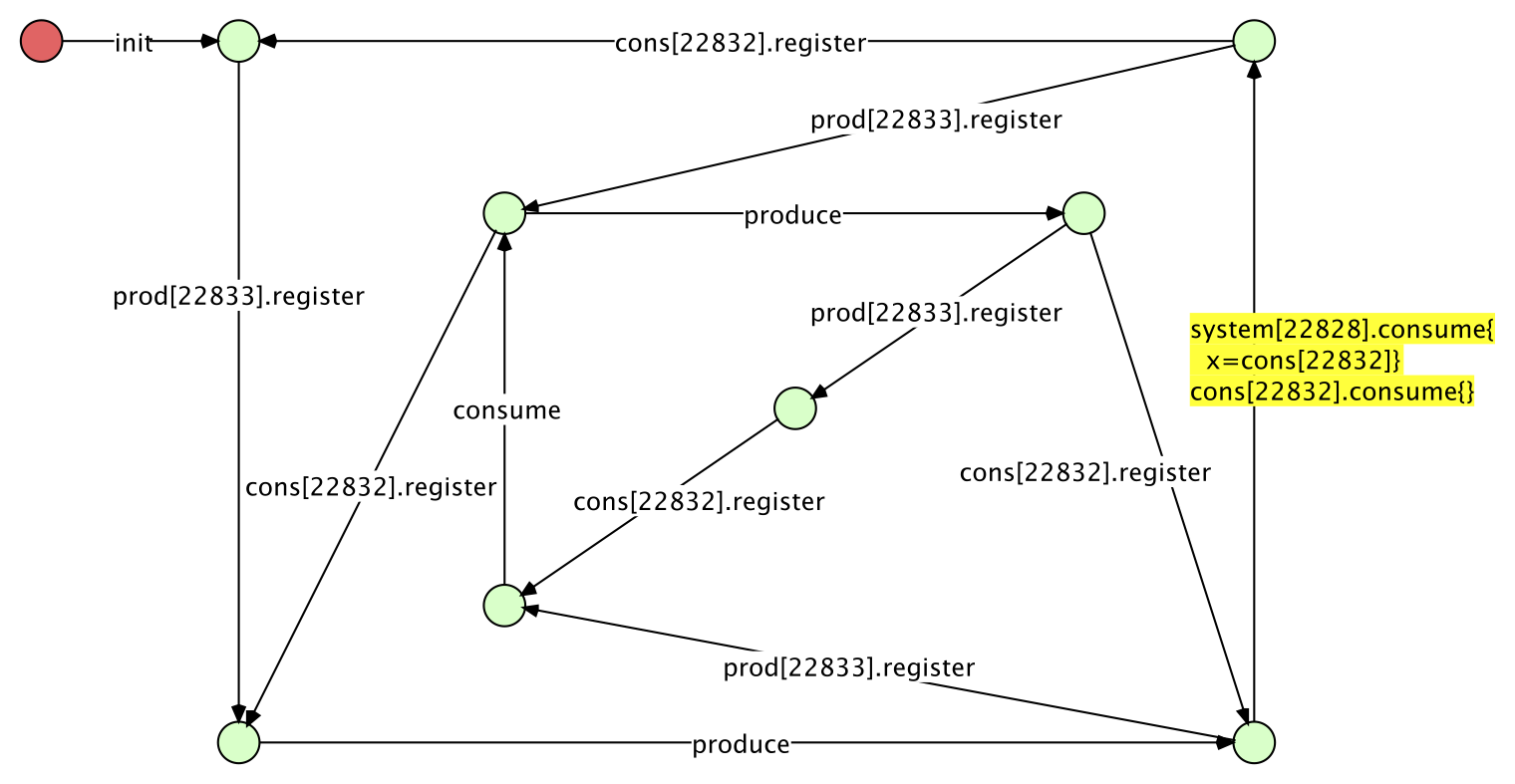
The ReferenceNetsReachabilityGraph Plugin is started with the system net as the root net. As the synchronous calls are initiated from the system net, they are listed without a prefix. The internal marking changes of the producer/consumer have the net instance ID as prefix.
The edge inscription with the yellow background has been extended to display the complete binding. The transition is a firing of the root net transition "consume", which is a synchronous channel. Therefore, also the corresponding transition in the consumer net instance is listed.
As mentioned before, node inscriptions would be more confusing than helpful. The plugin intends the interactive inspection of the graph. The following images show the inspection of the bottom right marking. The producer is back in his idle state whereas the the consumer is still in his waiting state and the storage is filled.
Note: The IDs of the net instances in the inspection differ from the IDs in the reachability graph, because they were inspected in a later simulation. Within a single execution of the plugin the IDs do not differ.
A More Complex Example
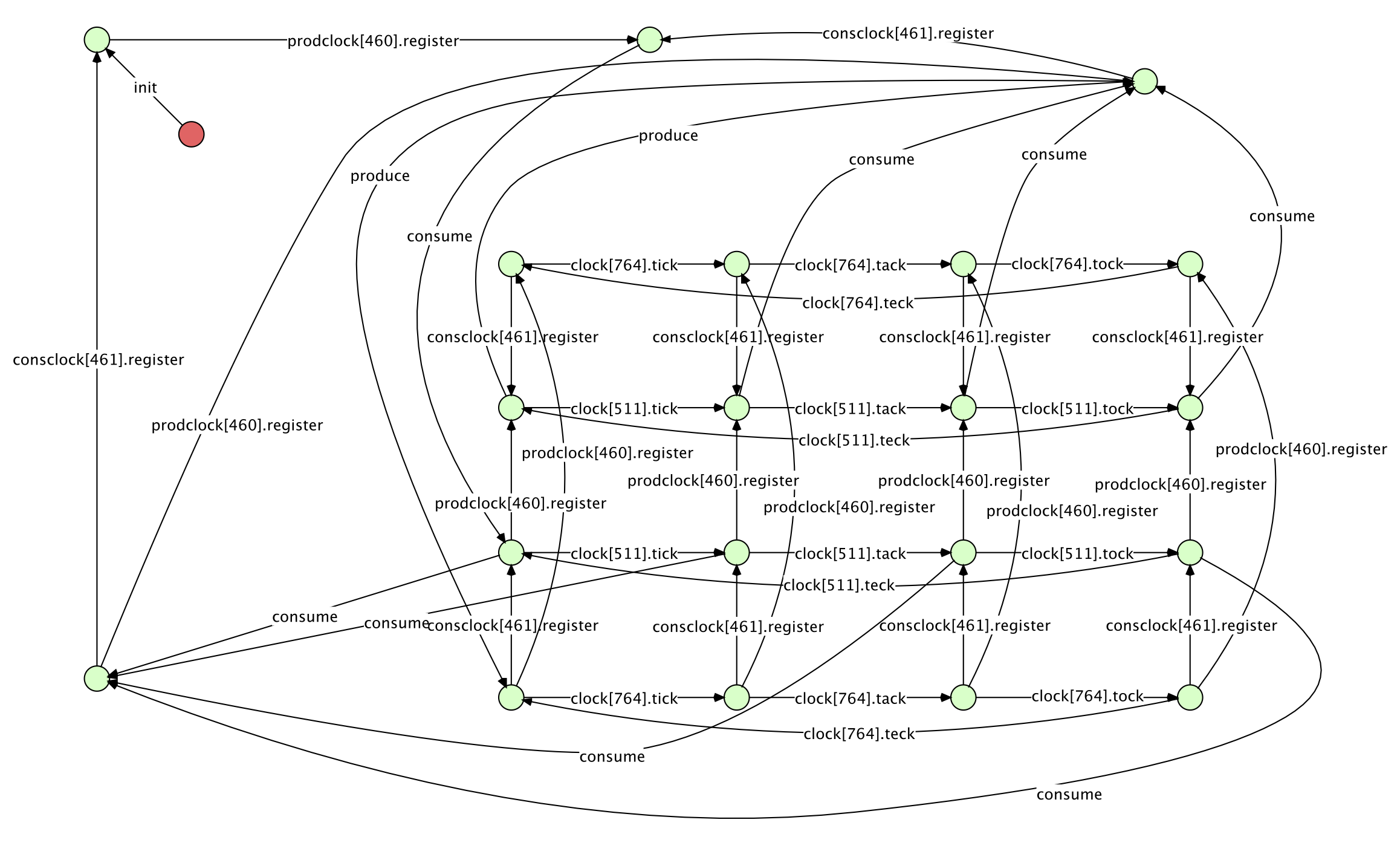
The following example extends the producer consumer problem by an actual product subnet. Instead of black tokens, the producer creates a clock net instance. This (simple) clock has four internal states. The transitions can fire concurrently to any other transition that is not in this net instance. The model is further simplified by assuming that the consumer instantly destroys the clock and therefore never has a persistent reference on it.
The net System
The Reachability Graph
As expected, the internal state of the clock leads to a significantly increased amount of distinct markings. This is even the case with only a single clock instance at a time that is not stored by the consumer. Still, the reachability graph becomes extremely hard to read for the human eye, even with proper formatting of the graph.
However, the complexity of the actual system that is being modeled did not really increase and is, in fact, still easy to describe in words. A proposed solution to this discrepancy is the feature to abstract certain nets or parts of their markings. The result is a folded reachability graph, where nodes that only differ in a marking of places that are flagged as "ignore" are folded into a single node. It is important to maintain the flexibility to flag only certain subnets, since in many cases, some subnets' behavior should be fully represented in the reachability graph, while others' should not.
Attachments (25)
- rw-rggraph.pdf (90.5 KB) - added by 6 years ago.
- rw-rggraph-depthlimit.pdf (74.8 KB) - added by 6 years ago.
- rw-net.pdf (30.6 KB) - added by 6 years ago.
- prodcons-complete.pdf (107.9 KB) - added by 6 years ago.
- prod-cons-rg-2.pdf (139.0 KB) - added by 6 years ago.
- prod-cons-rg-sys.png (37.1 KB) - added by 6 years ago.
- prod-cons-rg-cons.png (24.2 KB) - added by 6 years ago.
- prod-cons-rg-prod.png (24.3 KB) - added by 6 years ago.
- rw-counter-net.pdf (38.3 KB) - added by 6 years ago.
- rw-counter-rggraph.pdf (284.6 KB) - added by 6 years ago.
- prodcons-clockRG.pdf (364.8 KB) - added by 6 years ago.
- prodconsclock-complete.pdf (131.8 KB) - added by 6 years ago.
- prod-cons-rg-2.png (144.1 KB) - added by 6 years ago.
- prodcons-clockRG.png (426.7 KB) - added by 6 years ago.
- prodconsclock-complete.png (177.9 KB) - added by 6 years ago.
- rw-counter-net.png (77.5 KB) - added by 6 years ago.
- rw-counter-rggraph.png (221.1 KB) - added by 6 years ago.
- rw-net.png (56.6 KB) - added by 6 years ago.
- rw-rggraph.png (83.8 KB) - added by 6 years ago.
- rw-rggraph-depthlimit.png (76.9 KB) - added by 6 years ago.
- prodcons-complete.png (138.5 KB) - added by 6 years ago.
- fireNetsMarking.png (168.2 KB) - added by 6 years ago.
- fireNetsBundled.png (243.9 KB) - added by 6 years ago.
- fireRG.png (521.5 KB) - added by 6 years ago.
- rnrg_gui.png (33.8 KB) - added by 6 years ago.
![(please configure the [header_logo] section in trac.ini)](/paose/chrome/site/perspectives-logo-nb-text4-small.png)